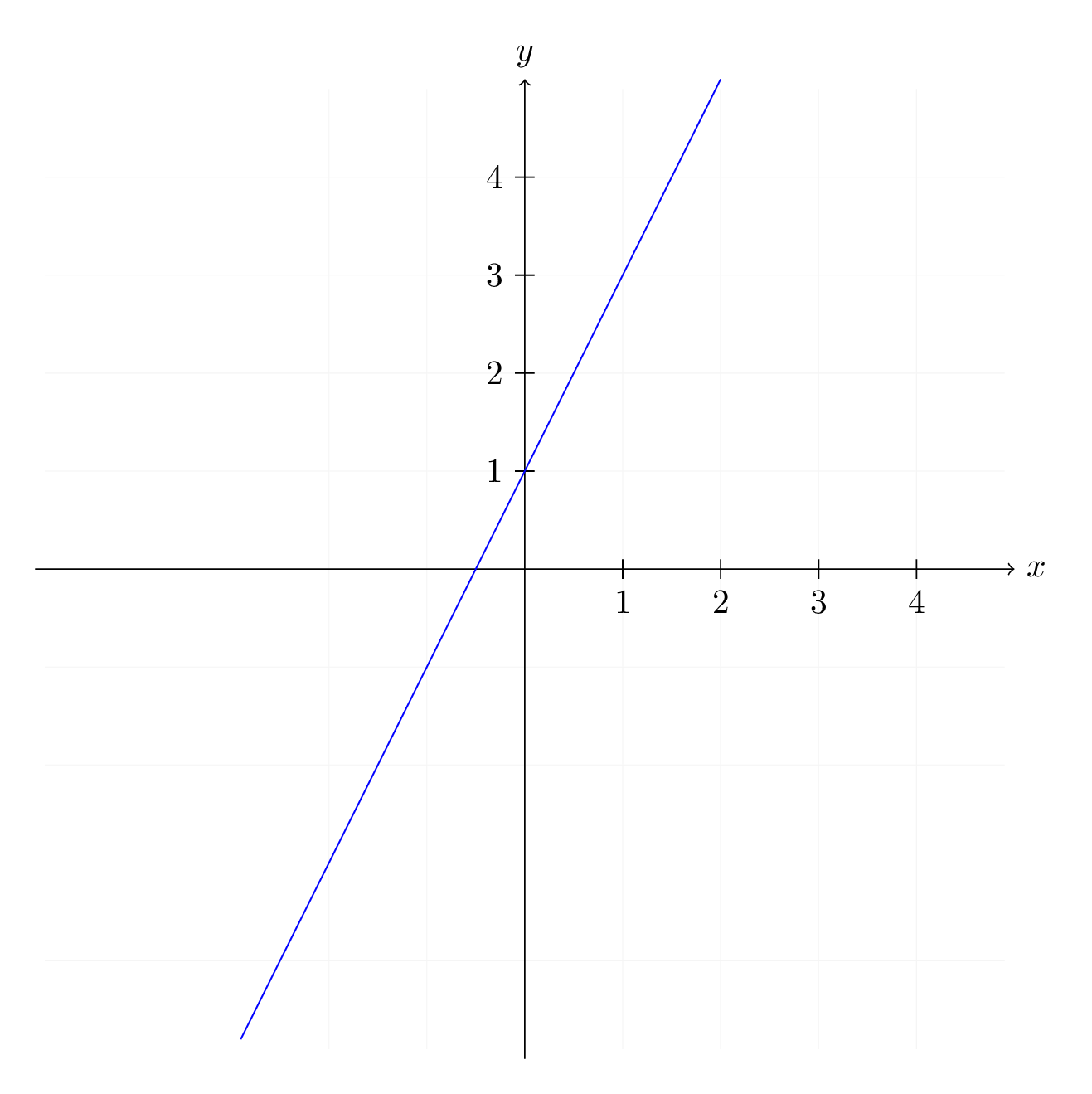Esempi e funzioni reali

La maggior parte delle funzioni che studiamo sono funzioni reali di variabile reale ovvero funzioni in cui il dominio è l’insieme dei numeri reali \(\mathbb R\) (o un suo sottoinsieme) mentre il codominio è sempre \(\mathbb R\) o un suo sottoinsieme.

$$f: A \to B \quad con \quad A \subseteq \mathbb R, \; B\subseteq \mathbb R$$

Tali funzioni, vedremo, si possono rappresentare con un grafico sul piano cartesiano.

Esempi

1)     \( \begin{align}  f: \mathbb R &\to \mathbb R \\  x &\mapsto x  \end{align} \)

Ovvero la funzione di equazione \(f(x)=x\).

Si tratta della funzione identità, una delle più semplici possibili. Infatti essa altro non fa che associare ad un numero \(x\) il numero \(x\) stesso (ad esempio a 3 associa 3 ( \(f(3)=3\) ), a \(\frac{3}{2}\) associa \(\frac{3}{2}\) e così via).

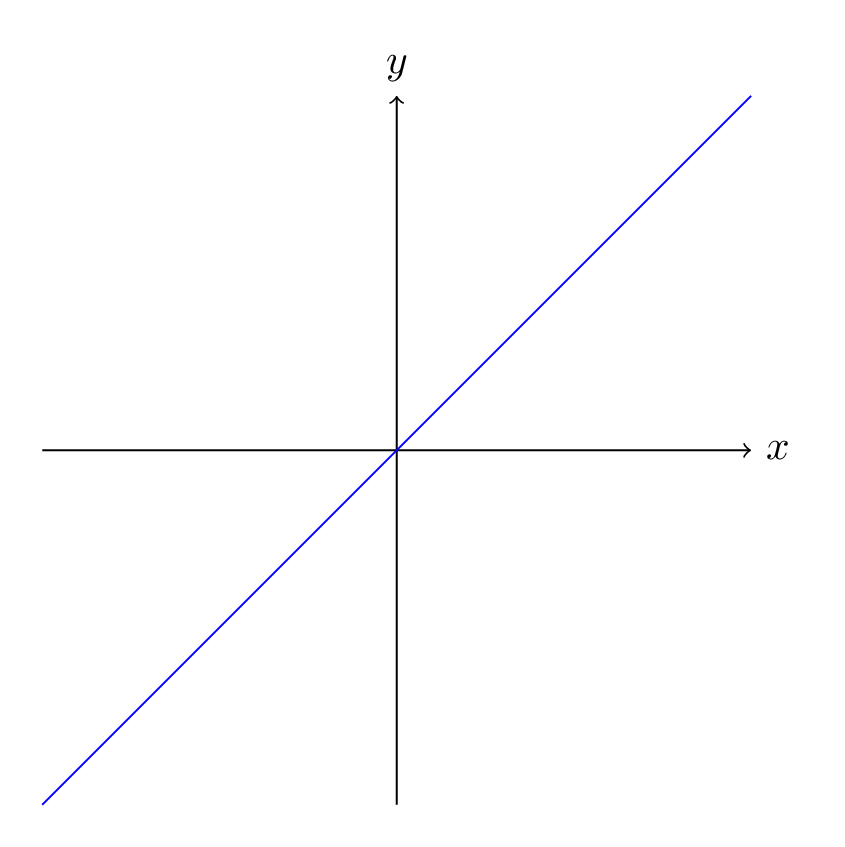
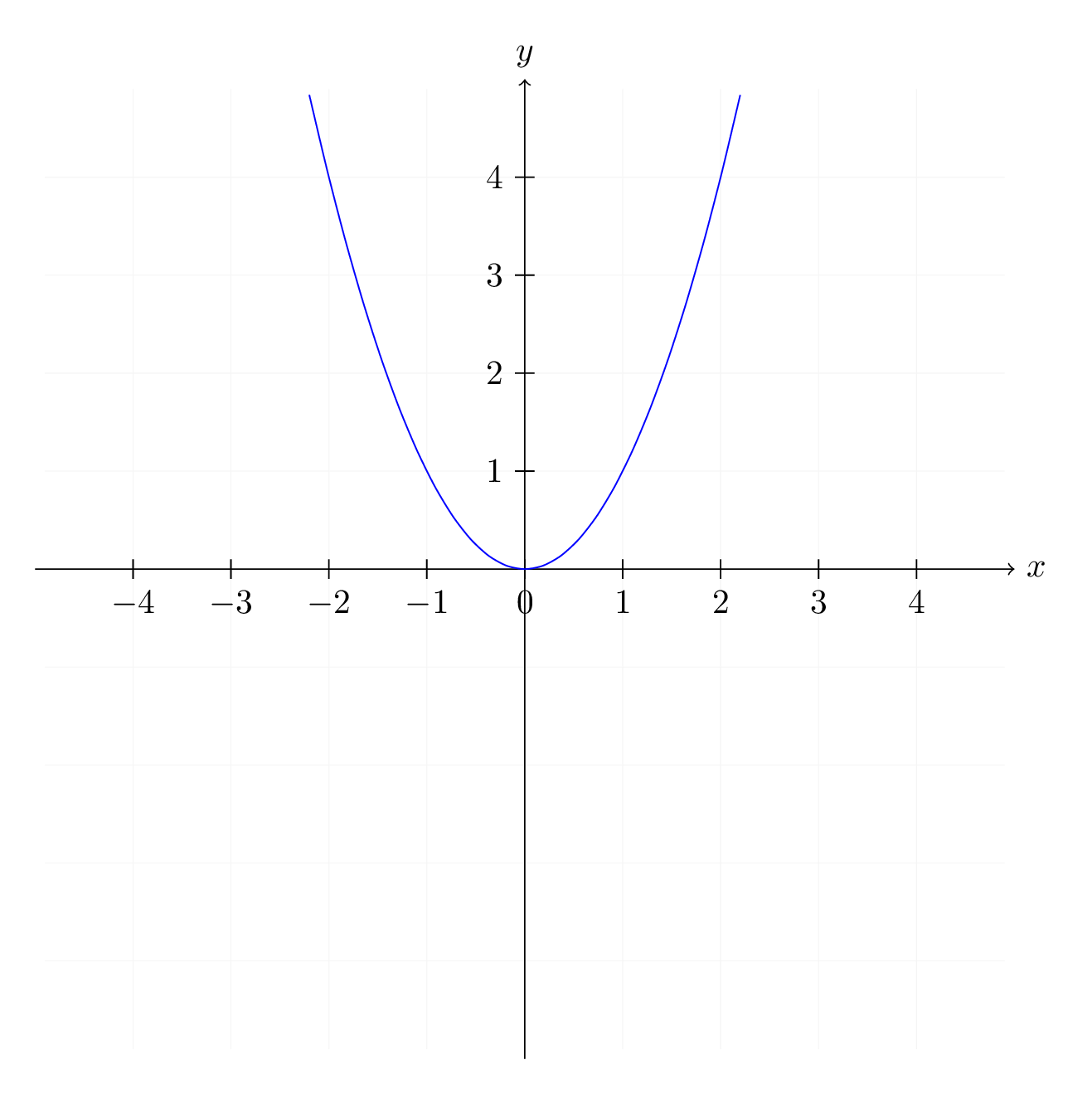
2)      \( \begin{align}  f: \mathbb R &\to \mathbb R \\  x &\mapsto x^2   \end{align} \)

Ovvero la funzione di equazione \(f(x)=x^2\).

È la funzione che ad ogni \(x \in \mathbb R\) associa il suo quadrato (ad esempio \(f(2)=4\), \(f(3)=9\), \(f(\pi)={\pi}^2\) e così via)  

3)      \( \begin{align}  f: \mathbb R &\to \mathbb R \\  x &\mapsto 2x+1  \end{align} \)

Ovvero la funzione di equazione \(f(x)=2x+1\).

Si tratta di una funzione lineare e infatti il suo grafico è una retta (come si è studiato in geometria analitica). Ad esempio valutando la funzione in alcuni punti si ottiene \(f(1)=3\), \(f(2)=5\) e così via.